Raymond Ian Gilbert只是在正式表达时才这么写，多数时候写为Gilbert R. I.， 我们平时就叫他Gilbert吧。我没查过他的生平，但估计年纪不小了，可能快80岁了，一直在澳大利亚教书。
最初知道他是因为看到了他写的一本书——Time Effects of Concrete Structures，这本出版于1984年著作后来再版时换了个新名子——Time-Dependent Behaviour of Concrete Structures。作者又增加了一位：Gianluca Ranzi。
关于混凝土结构力学性能的著作汗牛充栋，但我将阅读Gilbert视为一条捷径，我只找了几篇他的文献各位参考：下载地址。
本帖是吉尔伯特所著《混凝土结构时随性能》的笔记。
在钢筋混凝土构件强度计算中，混凝土的抗拉能力一般被忽略。尽管由于受拉钢筋会因为混凝土粘结将力传给混凝土，混凝土还会因此持续承担拉应力。受拉混凝土这一贡献即为拉力刚化，它影响着开裂后构件的刚度，也因此影响了变形和裂缝的宽度。
钢筋混凝土构件经常会含有相对少量的受拉钢筋，某些情况下接近于规范容许的最小量。在楼板中经常是这种情况。对于此类构件，完全开裂截面的抗弯刚度(E_cI_{cr})比未开裂截面刚度(E_cI_{uncr})小很多倍，拉力刚化效应对于开裂后构件刚度贡献很大。在结构设计中，在服役荷载水平下变形和开裂控制通常成为控制因素，需要对开裂后刚度准确建立模型。
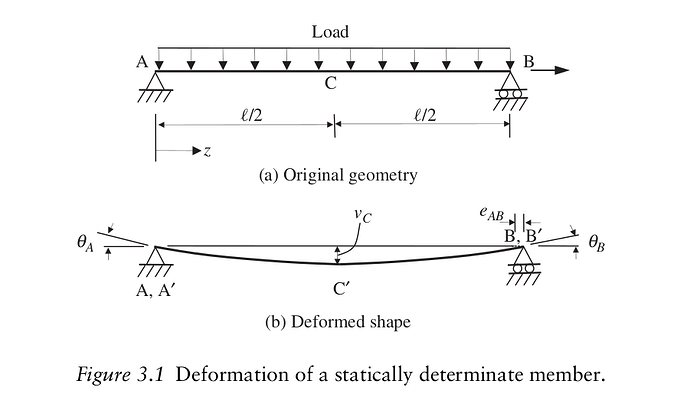
若构件某区段内的轴向应变和曲率已知，计算该构件的变形是相对简单的任务。考查图3.1中承受轴力和横向荷载的静定结构。构件的轴向变形 e_{AB} (伸长或缩短)可由沿构件中心的应变 \varepsilon_{a} 积分得到：
式中$z$是延构件长度的度量。
假设变形很小，简化梁理论适用，则任意点 z 处的转角 \theta 和变形 \upsilon 可通过曲率 \kappa(z) 延构件积分如下：
上述式子十分通用，可应用于弹性和非弹性材料行为。
如果轴向应变和曲率在构件上预先选定的点上做了计算，且假定在相邻点间的应变和曲率变化做了合理的假设，则用简单的几何积分即可确定构件的变形。为便于应用，下面给出了简支跨和悬臂梁变形计算的公式。若构件端点和跨中的应变 \varepsilon_a 和曲率 \kappa 已知，则可知轴向变形 e_{AB} 和支点转角 \theta_A 和 \theta_B 和跨中挠度 \upsilon_C ：
当应变和曲率线性变化时：
(本节后文略)
